Оптимизация – это целенаправленная деятельность, заключающаяся в получении наилучших результатов при соответствующих условиях. В математике оптимизация связана с нахождением оптимума (т.е. максимума или минимума) некоторой функции.
Если рассматриваемая функция является функцией одной переменной, в этом случае говорят об одномерной оптимизации.
Если на значения аргументов налагаются ограничения в виде равенств или неравенств, то такие задачи называют условными задачами оптимизации или задачами с ограничениями. В противном случае имеем задачу безусловной оптимизации.
Несмотря на то, что безусловная оптимизация функции одной переменной наиболее простой тип оптимизационных задач, она занимает центральное место в теории оптимизации как с теоретической, так и с практической точек зрения. Это связано с тем, что задачи однопараметрической оптимизации достаточно часто встречаются в инженерной практике и, кроме того, находят свое применение при реализации более сложных итерактивных процедур многопараметрической оптимизации.

Для определенности будем считать, что решаем задачу отыскания минимума функции y = f(x) на интервале (a; b).

2.2. Метод сканирования.

Интервал поиска (a; b) разбивается на несколько равных участков, каждый из которых равен шагу поиска h(рис. 1).
Рис. 1. Метод локализации.

Далее последовательно определяются значения функции f(x) во всех точках разбиения аргумента и в точках a и b и запоминается наименьшее значение. Таким образом, минимум может быть найден с точностью до h.
Достоинства метода: простота, возможность нахождения глобального минимума.
Недостаток метода: большой объем вычислений.
Пример. Найти минимум функции  с точностью ε = 0,3 на интервале (-2; 1)
Решение. Точность ε = 0,3 - шаг поиска. Количество частей разбиения интервала
, где […] обозначают целую часть выражения, записанного в скобках.
n = 10.

Наименьшее значение функции: -0,99.
Точка минимума: -1,1.

2.3. Метод локализации.

Алгоритм метода:

1. Интервал поиска минимума (a; b) разбивается на четыре равные части точками x1, x2, x3.
2. Вычисляются значения функции y = f(x) во всех точках разбиения и в точках x = a, x = b.
3. Полученные значения f(x) сравниваются между собой, и из них выбирается наименьшее.
4. Локализуется минимум, причем новый интервал поиска равен двум старым подинтервалам с наименьшим значением f(x) на их общей границе (на рис. 2 это соответствует интервалу (a, x2)).
5. Интервал, в котором локализован минимум, опять делится на четыре равных подынтервала ( на рис. 2 точками x4, x5) и снова вычисляются значения функции y = f(x) в точках деления. Они сравниваются между собой, находится наименьшее, локализуется минимум в меньшем интервале ( на рис. 2 в интервале (x4, x5)) и так далее до тех пор, пока минимум не будет локализован в интервале, размер которого соответствует заданной точности поиска.

Замечание.Интервал, поиска разбивается именно на четыре, подынтервала с целью уменьшения объема вычислений: при этом каждый последующий подынтервал делится пополам, и вычислять значение функции нужно только в двух новых точках, так как её значения на концах нового интервала и в его середине известны из предыдущих расчетов.

2.4. Метод золотого сечения.

При построении процесса оптимизации стараются сократить объем вычислений и время поиска. Этого достигают обычно путем сокращения количества вычислений значений функции y = f(x). Одним из наиболее эффективных методов, в которых при ограниченном количестве вычислений f(x) достигается наилучшая точность, является метод золотого сечения.
Если известно, что функция f(x) имеет только один минимум на отрезке [a; b], то положение точки минимума можно уточнить, вычисливf(x) в двух внутренних точках отрезка. При этом возможны две ситуации:
1. . Минимум реализуется на отрезке [a; x2].


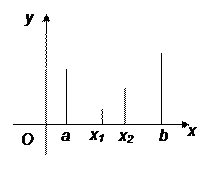
2. . Минимум реализуется на отрезке [x1; b].

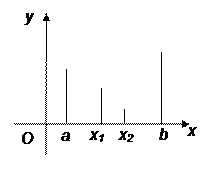
В методе золотого сечения каждая из точек x1 и x2 делит исходный интервал на две части так, что отношение целого к большей части равно отношению большей части к меньшей, т.е. равно так называемому «золотому отношению». Это соответствует следующему геометрическому представлению:

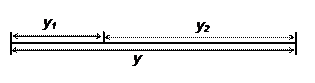
Здесь  или . Обозначим , получим . Решив данное уравнение, получим . Итак, длины отрезков [a, x1] и [x2, b] одинаковы и составляют 0,382 от длины (a, b). По значениям f(x1) и f(x2) определяется новый интервал (a, x2) или (x2, b), в котором локализован минимум. Найденный интервал снова делится двумя точками в том же отношении, причем одна из новых точек деления совпадает с уже использованной на предыдущем шаге.
Таким образом, длина интервала неопределенности на каждом шаге сжимается с коэффициентом 0,618. На первом шаге необходимы два вычисления функции, на каждом последующем – одно.
Алгоритм метода золотого сечения для минимизации функции.

1. Вычисляется значение функции f(x1), где x1 = a + 0,382(b - a).
2. Вычисляется значение функции f(x2), где x2 = b - 0,382(b - a).
3. Определяется новый интервал (a, x2) или (x2, b), в котором локализован минимум.
4. Внутри полученного интервала находится новая точка (x1 в случае 1) или (x2в случае 2), отстоящая от его конца на расстоянии, составляющем 0,382 от его длины. В этой точке рассчитывается значение f(x). Затем вычисления повторяются,начиная с пункта 3, до тех пор, пока величина интервала неопределенности станет меньше или равна ε, где ε - заданное сколь угодно малое положительное число.

program one;
var x,y,a,b,e,ymin,ymax,n:real; k:integer;
begin

writeln('vvedi nachalo intervala');
readln(a);
writeln('vvedi konec intervala');
readln(b);
writeln('vvedi tochnost ');
readln(e);
n:=((b-a)/e)+1;
writeln('kolichestvo chastey', n);
x:=a;
y:=x*x + 2*x;
writeln('y o =', y);
ymin:=y;
k:=1;
while k <> n-1 do
begin
x:=x+e;
y:=x*x + 2*x;
if ymin > y then ymin:=y
else ymax:=y;
k:=k+1;
end;
writeln('maksimym funkcii', ymax);
writeln ('minimum funkcii', ymin);
end.

program two;
var x,y,e,n,x1,x2,x3,a,b,ya,yb,y1,y2,y3, ym:real;
begin

writeln('vvedi nachalo intervala');
readln(a);
writeln('vvedi konec intervala');
readln(b);
ym:=100;

writeln('vvedi tochnost ');
readln(e);
while (b-a)> e do begin
ya:=a*a+ 2;
yb:=b*b + 2;
x1:= a+(b-a)/2;
y1:=x1*x1 + 2;
x2:=a+(x1-a)/2;
y2:=x2*x2 + 2;
x3:=x1+(b-x1)/2;
y3:=x3*x3 + 2;{
writeln(ya,' ',yb,' ',y1, ' ',y2,' ',y3);}

if y2<ym then begin ym:=y2; a:=a; b:= x1; end else
if y1<ym then begin ym:=y1; a:=x2; b:= x3; end else
if y3<ym then begin ym:=y3; a:=x1; b:= b; end else
if yb<ym then begin ym:=yb; b:= b+ (b-x3) ;a:= x3; {writeln('not_2!'} end else
if ya<ym then begin ym:=ya; a:=a-(x2-a); b:= x2 end;
{writeln('not_1!');}
end;
writeln('ymin = ',ym);
end.

program three;
var
a1,a2,y,x,e,k2,k,y1,y2,b1,b2: real;
begin
k:=100;
writeln('введите промежуток');
read(a1,b1);
{y:=x+4;}
e:=0.01;
a2:= a1+(0.382*(b1-a1));
b2:=b1-(0.382*(b1-a1));
while abs(k)>e do begin
y1:=-a2+4;
y2:=-b2+4;
if y1<y2 then begin
b1:=b2;
b2:=a2;
a2:= a1+(0.382*(b1-a1));
k:=b2-a1;
y:=y1; end
else begin
a1:=a2;
a2:=b2;
b2:=b1-(0.382*(b1-a1));
k:=b1-a2;
y:=y2; end;
end;
writeln(y:2:2);
end.