Среднее значение

Среднеквадрати́ческое отклоне́ние (синонимы: среднеквадрати́чное отклоне́ние, квадрати́чное отклоне́ние; близкие (но не совпадающие) термины: станда́ртное отклоне́ние, станда́ртный разбро́с) — в теории вероятностей и статистике наиболее распространённый показатель рассеивания значений случайной величины относительно её математического ожидания.

Основные сведения

Измеряется в единицах измерения самой случайной величины. Равно корню квадратному из дисперсии случайной величины. Среднеквадратичное отклонение используют при расчёте стандартной ошибки среднего арифметического, при построении доверительных интервалов, при статистической проверке гипотез, при измерении линейной взаимосвязи между случайными величинами.

Среднеквадратичное отклонение:

$\sigma=\sqrt{\frac{1}{n}\sum_{i=1}^n\left(x_i-\bar{x}\right)^2};$

стандартное отклонение (несмещённая оценка среднеквадратичного отклонения случайной величины x относительно её математического ожидания):

$s=\sqrt{\frac{n}{n-1}\sigma^2}=\sqrt{\frac{1}{n-1}\sum_{i=1}^n\left(x_i-\bar{x}\right)^2};$

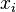где $\sigma^2\,\!$ — дисперсия; $x_i\,\!$ — i-й элемент выборки; $n\,\!$ — объём выборки; $\bar{x}\,\!$ — среднее арифметическое выборки:

$\bar{x} = \frac{1}{n}\sum_{i=1}^n x_i = \frac{1}{n} (x_1+\cdots+x_n).$

Следует отметить отличие стандартного отклонения (в знаменателе n − 1) от корня из дисперсии (среднеквадратичного отклонения) (в знаменателе n). При малом объёме выборки оценка дисперсии через последнюю величину является несколько смещённой, при бесконечно большом объёме выборки разница между указанными величинами исчезает.

program srednee;
uses crt;
type vektor=array[1..500] of real;
var
M: vektor;
f: text;
N,i: integer;
myu,sigma: real;
function SUM(N1: integer; M1: vektor): real;
var i1: integer;
S1: real;
begin
S1:=0;
for i1:=1 to N1 do S1:=S1+M1[i1];
SUM:=S1;
end;
function SUM2(N1: integer; M1: vektor; myu1: real): real;
var i1: integer;
S1: real;
begin
S1:=0;
for i1:=1 to N1 do S1:=S1+sqr(M1[i1]-myu1);
SUM2:=S1;
end;

begin
clrscr;
WriteLn('Vvedite N');
Read(N);
Assign(f,'input.txt');
Reset(f);
for i:=1 to N do
ReadLn(f,M[i]);
Close(f);
myu:=(1/N)*SUM(N,M);
WriteLn('Srednee znachenie=', myu:0:4);
sigma:=sqrt((SUM2(N,M,myu))/(N-1));
WriteLn('Srednekvadraticheskoe otklonenie=', sigma:0:4);
ReadLn;
ReadLn;
end.

Среднеквадратическое отклонение

Основные сведения