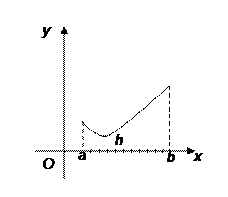
Интервал поиска (a; b) разбивается на несколько равных участков, каждый из которых равен шагу поиска h(рис. 1).
Оптимизационные задачи
Оптимизация – это целенаправленная деятельность, заключающаяся в получении наилучших результатов при соответствующих условиях. В математике оптимизация связана с нахождением оптимума (т.е. максимума или минимума) некоторой функции.
Если рассматриваемая функция является функцией одной переменной, в этом случае говорят об одномерной оптимизации.
Если на значения аргументов налагаются ограничения в виде равенств или неравенств, то такие задачи называют условными задачами оптимизации или задачами с ограничениями. В противном случае имеем задачу безусловной оптимизации.
Несмотря на то, что безусловная оптимизация функции одной переменной наиболее простой тип оптимизационных задач, она занимает центральное место в теории оптимизации как с теоретической, так и с практической точек зрения. Это связано с тем, что задачи однопараметрической оптимизации достаточно часто встречаются в инженерной практике и, кроме того, находят свое применение при реализации более сложных итерактивных процедур многопараметрической оптимизации.
Для определенности будем считать, что решаем задачу отыскания минимума функции y = f(x) на интервале (a; b).
Пути решения:
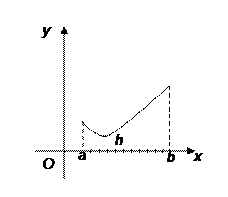
Интервал поиска (a; b) разбивается на несколько равных участков, каждый из которых равен шагу поиска h(рис. 1).
![]() Рис. 1. Метод локализации.
Рис. 1. Метод локализации.
Далее последовательно определяются значения функции f(x) во всех точках разбиения аргумента и в точках a и b и запоминается наименьшее значение. Таким образом, минимум может быть найден с точностью до h.
Достоинства метода: простота, возможность нахождения глобального минимума.
Недостаток метода: большой объем вычислений.
Алгоритм метода:
Замечание.Интервал, поиска разбивается именно на четыре, подынтервала с целью уменьшения объема вычислений: при этом каждый последующий подынтервал делится пополам, и вычислять значение функции нужно только в двух новых точках, так как её значения на концах нового интервала и в его середине известны из предыдущих расчетов.
Алгоритм метода золотого сечения для минимизации функции.